Skip to main content

Chimie

Modèle de lewis et autres

  • Formule brute :

$$ C_4NH_{11} $$

  • Formule développée (lewis) :

Formule déveoppée

  • Formule semi-développée :
CH3 --- CH2 --- CH2 --- CH2 --- NH2
  • Modèle de Bohr :

Modèle de Bohr, wikimedia Les électrons qui sont sur la dernière couche sont les électrons de valence, ceux qui peuvent faire des liaisons chimiques.

Types de liaisons

Trouver le delta de l'électro négativité : électronégativité du premier élément - électronégativité d'un deuxième

Pour connaitre le type de liaison, il faut utiliser le barème suivant avec le delta de l'électronégativité

0          0.5        1.7        2          ...
|__________|__________|__________|__________|
 covalente  covalente    ↓ ↓ ↓     ionique
 non-polar  polarisée
  • Entre 0 et 0.5, la liaison est covalente non-polaire, aussi appellé liaison "pure"
  • Entre 0.5 et 1.7, la liaison est covalente polarisée
  • Entre 1.7 et 2, si c'est une liaison entre 2 métaux, la liaison est ionique, sinon la liaison est covalente polarisée
  • Plus de 2, la liaison est ionique

Représentation spaciale

En utilisant la représentation de Cram on peut représenter une molécule dans l'espace (en 3D) sur un plan en 2D.

ImageDescription
Liaison dans le plan
Liaison en avant du plan
Liaison en arrière du plan

Voici un exemple de représentation pour une molécule tétrahédrique:

Configuration spaciale VSEPR et son comportement dans l'eau

A FAIRE

Configurationpolaire/apolairecomportement dans l'eau
Thétrahédriqueapolairehétérogène
Coudéepolairehomogène
Linaireapolairehétérogène

Equation de dissociation des sels 

  • Voici la formule de la dissociation d'un sel binaire

$$ MX_{(aq)} → M_{(aq)}^+ + X_{(aq)}^- $$

  • Voici la formule de la dissociation d'un sel tertiaire

$$ MXO_{(aq)} → M_{(aq)}^+ + XO_{(aq)}^- $$

$M$ veut dire "métal" et $X$ veut dire "non-métal" et $O$ est tout simplement l'oxygène.

Voici un exemple avec $NaCl$ en sachant que $Na$ est un métal et $Cl$ est un non-métal. C'est donc un sel binaire et sa formule de dissociation dans l'eau est la suivante.

$$ NaCl_{(aq)} → Na_{(aq)}^+ + Cl_{(aq)}^- $$

Constante d'équilibre et concentration molaire

La concentration molaire est le nombre de mol par litre et son unité est le $mol/L$ sa formule est $\frac{n}{V}$.

La constante d'équilibre caractérise l'état d'équillibre d'une réaction chimique et est régie par la température, son unité est le $mol/L$ et sa formule est la suivante :

Pour la formule brute suivnte : $aA + bB → cC + dD$ : $Kc = \frac{[C]^c * [D]^d}{[A]^a * [B]^b}$ (à savoir que les crochets signifie la concentration molaire).

Réaction complète et incomplète

Une réaction complète c'est quand il ne reste aucun réactifs à la fin de la réaction.

Une réaction incomplète ou limitée c'est quand il reste un réactif à la fin de la réaction.

Sens des réactions

Chimie organique

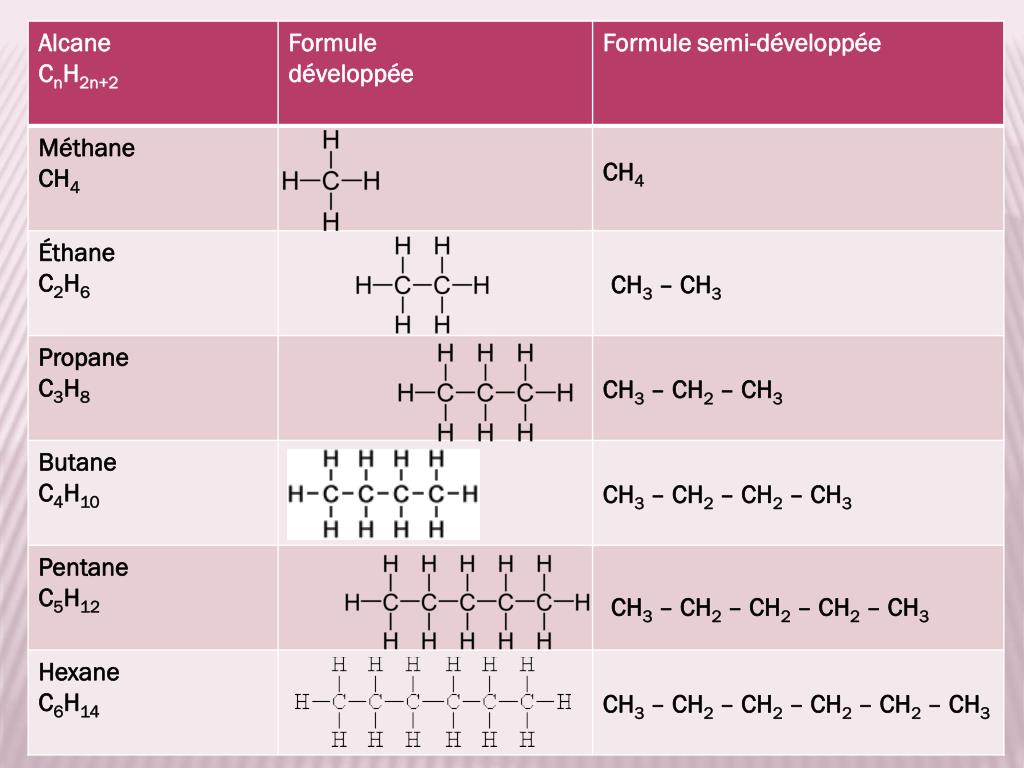
alcanes

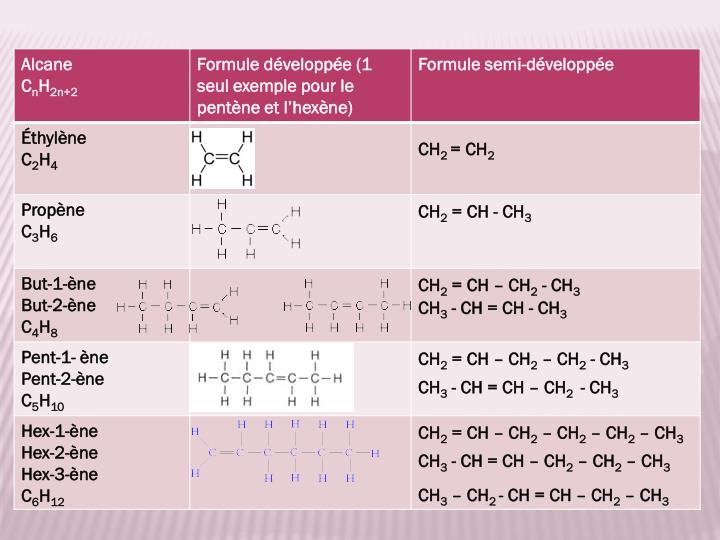
alcène

Combustion

ExemmpleDescription
$C_3H_8$Faire la combustion du propane
$C_3H_8 + O_2 → CO_2 + H_2O$La mettre dans l'équation de combustion complète
$C_3H_8 + 2O_2 → 3CO_2 + 4H_2O$Pondérer l'équation (d'abord les $C$, puis les $H$ et puis les $O$)

pH

$$ -\log{[H_3O^+]} $$

$[H_3O^+]$ est l'ion hydronium.

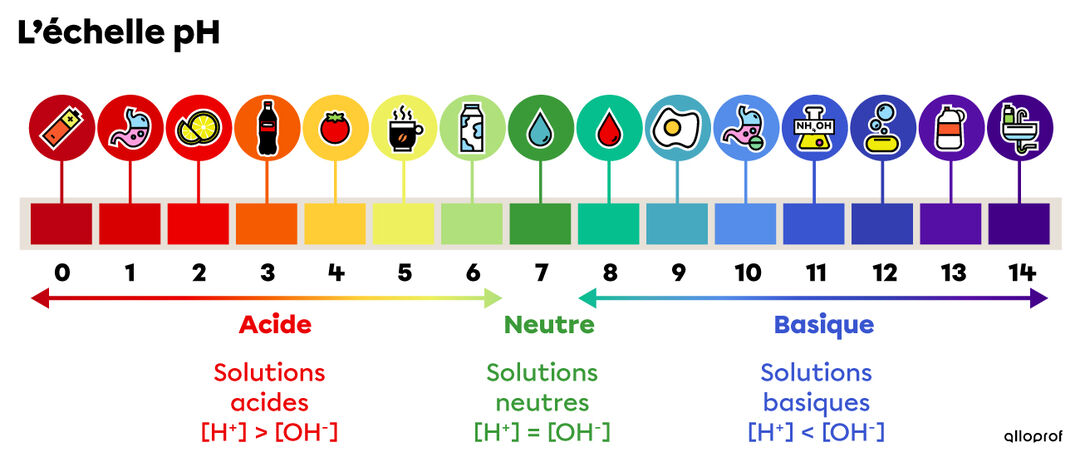
Équations ioniques

Incertain

ExempleExplication
$H_2SO_4$ et $NaOH$Énoncé
$H_2SO_{4 (aq)} + NaOH_{(aq)}$Mettre les 2 molécules ensemble et sous forme aqueuse (dissous dans l'eau)
$H_2SO_{4 (aq)} + NaOH_{(aq)} → H_2O_{(l)} + Na_2SO_{4 (aq)}$Combiner les cations et les anions ($H^+$ et $OH^-$ donne $H_2O$ / $Na^+$ et $SO_4^{2-}$ donnent $Na_2SO_4$)$
$H_2SO_{4 (aq)} + 2NaOH_{(aq)} → 2H_2O_{(l)} + Na_2SO_{4 (aq)}$Pondérer l'équation
$2H^+ + SO_4^{2-} + 2Na^+ + 2OH^- → 2Na^+ + SO_4^{2-} + 2H_2O_{(l)}$Décomposer l'équation en ions et pondérer la nouvelle équation
$2H^+ + 2OH^- → 2H_2O_{(l)}$Supprimer les doublons qui sont des 2 cotés de l'équation (ils sont les ions spectateurs)
$H^+ + OH^- → H_2O_{(l)}$Simplifier

Oxydoréduction

Faire une oxydoréduction de $Cu$ et $NO_3$

ExempleDescription
$Cu/Cu^{2+}$
 $NO/NO_3^-$		Trouver l'équivalent dans les cations et anions du tableau de solubilité
$Cu → Cu^{2+}$
 $NO → NO_3^-$		Equilibrer tous les éléments autre que O et H, dans ce cas il n'y a rien à équilibrer
$Cu → Cu^{2+}$
 $NO + 2H_2O → NO_3^-$		Equilibrer les $O$ en ajoutant des $H_2O$
$Cu → Cu^{2+}$
 $NO + 2H_2O → NO_3^- + 4H^+$		Equilibrer les $H$ en ajoutant des $H^+$
$Cu → Cu^{2+} + 2e^-$
 $NO + 2H_2O → NO_3^- + 4H^+ + 3e^-$		Equilibrer les charges en ajoutant des électrons
$3Cu → 3Cu^{2+} + 5e^-$ (multiplié par 3)
 $2NO + 4H_2O → 2NO_3^- + 4H^+ + 5e^-$ (multiplié par 2)		Multiplier toues les 2 demi-équations pour que les charges soit égales
$3Cu + 2NO_3^- + 4H^+ + 5e^- → 2NO + 4H_2O + 3Cu^{2+} + 5e^-$Mettre les deux demi-équations en une (voir gamma plus bas)
$3Cu + 2NO_3^- + 4H^+ → 2NO + 4H_2O + 3Cu^{2+}$Supprimer les électrons car égaux
  1. Équilibrer les autres éléments que O et H (pondération)
  2. Equilibrer les $O$ en ajoutant $H_2O$
  3. Équilibrer les H en ajoutant $H^+$
  4. Rétablir l'égalité des charges en ajoutant $e^-$
  5. Multiplier si charges différentes
  6. Écrire l'équation complète (gamma)
Back to top