Automates finis

Pour comprendre cette section, comprendre ce qu'est un diagramme d'état et ce que sont les langages formels est très utile.

Un automate fini est une construction mathématique abstraite représentant une machine ayant plusieurs états et des transitions permettant de passer d'un état à l'autre.

Les mécanismes

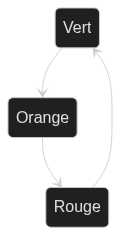
Les mécanismes sont des machines simples, sans inputs ni output et sans lien avec le monde extérieur. Elles ne sont dirigées que par leur propre horloge interne. En voici un exemple pour un feu tricolore :

Ils peuvent être décrits par le couple $M = (E, t)$ où E est l'ensemble des états et t la fonction de transition entre les états. Un premier état sera représenté par $e$ et à l'instant suivant passera dans l'état $t(e)$.

Les mécanismes seront toujours une boucle infinie, il n'y a pas de point de départ ni de point d'arrivée. Et si un état n'a des transitions qu'avec lui-même ou à personne, alors on dira que c'est un état repos.

Automates fini

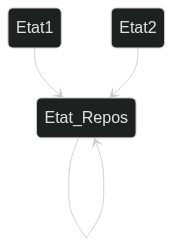
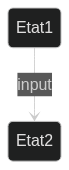
Les automates finis sont un peu plus complexes que les mécanismes, car ils ont des inputs. Un automate fini est décrit par le triplet $A = (E, \Sigma, t) où E est l'ensemble fini et non-vide des états, $\Sigma$ l'ensemble fini des inputs et t la fonction de transition.

Un état $e$ après l'ajout d'un input i deviendra $t(e,i)$. Un diagramme d'état d'un automate fini sera représenter comme ceci :

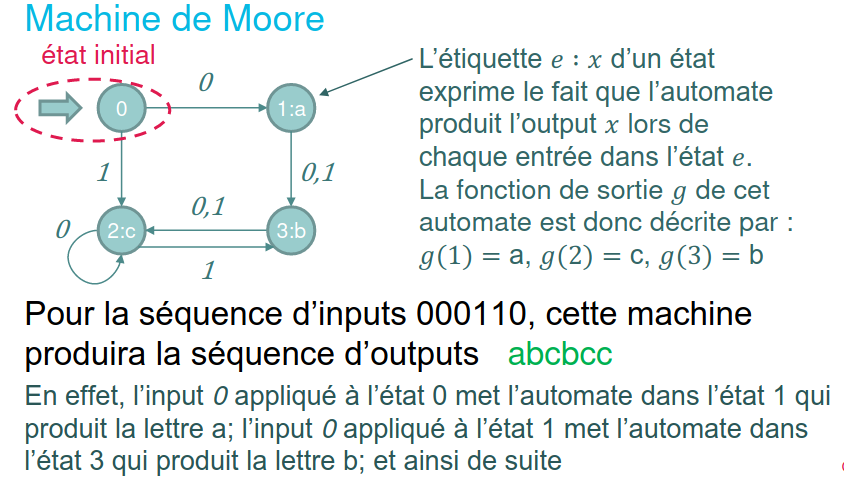
Machines de Moore et machines de Mealy

Les automates précédents ne servent pas à grand-chose, car ils ne produisent rien. Contrairement aux automates précédents, ceux-ci ont un état initial et une séquence d'output.

Les machines de Moore et de Mealy sont différentiées par ce qui détermine l'output :

Dans une machine de Moore, la sortie est déterminée par l'état après la transition

Dans une machine de Mealy, la sortie est déterminée par la transition elle-même

Les machines de Moore et Mealy sont des machines séquentielles qui transforment une suite (input) en une autre suite (outputs). Une machine de Moore est toujours un cas particulier de machine de Mealy et inversement une machine de Mealy a toujours une machine de Moore équivalente.

Machines de reconnaissance

Maintenant, on va s'intéresser à un type particulier de machine de Moore, les machines de reconnaissances. Elles ont comme seuls outputs 0 et 1. 0 si l'input n'est pas reconnu et 1 s'il l'est.

Par convention, un état non reconnu sera un simple rond, et un état reconnu (aussi appelé état d'acceptation) sera un double rond.

Cette machine va donc servir à vérifier si une séquence donnée mène ou non à un état d'acceptation.

Cet automate de Moore va être défini par le quintuplet $M = (E, \Sigma, t, e_0, A)$ où E est l'ensemble fini d'états, $\Sigma$ est l'ensemble des inputs (tel que l'alphabet dans le cas des langages formels), t est la fonction de transition d'un état à l'autre, $e_0$ est l'état initial et A est l'ensemble des états d'acceptations.

Dans le cadre des langages formels, tous les langages reconnus par une machine de Moore seront des grammaires de type 3 (langage régulier). Et on peut créer un automate à partir d'une grammaire ou une grammaire à partir d'un automate.

Comme vu à la page précédente, une grammaire d'un langage peut être définie comme étant $G = (\Sigma, N,P,S)$ où :

$\Sigma$ est l'alphabet (c'est-à-dire les inputs)
N l'ensemble des symboles non-terminaux (c'est-à-dire les états)
P sont les productions de la grammaire (l'équivalent des transitions entre les états)
S le symbole non terminal de départ (soit l'état initial)

Voici un automate représentant une grammaire (de type 3, soit régulière) avec la règle suivante "tout mot avec un nombre pair de a et strictement 1 b "

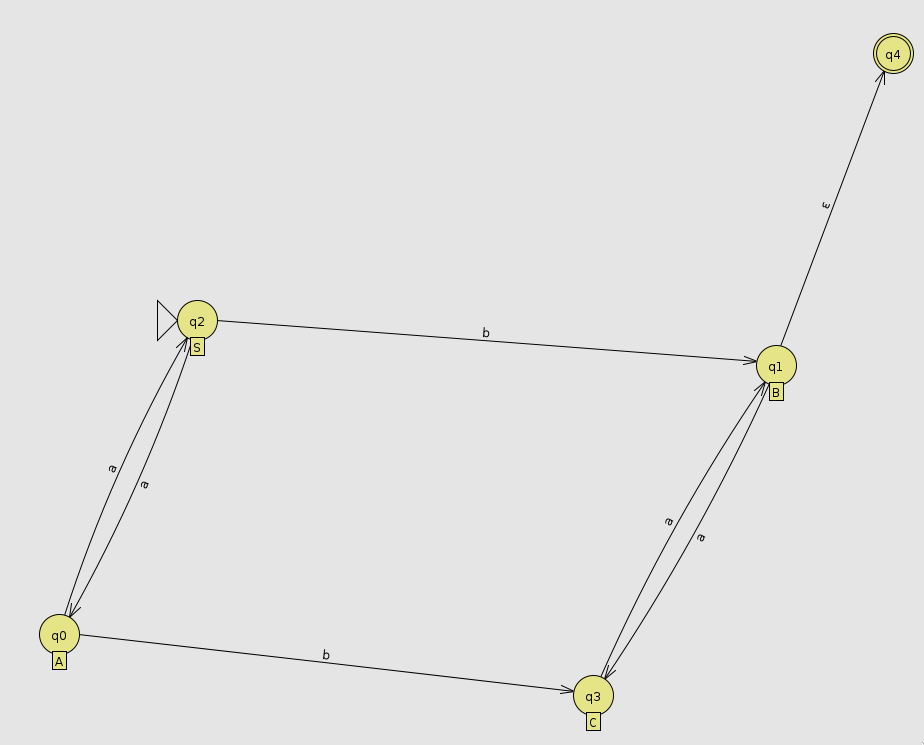Ici q4 est un état final, mais cet état aurait très bien pu être q1 (soit B)

Dans cet automate, les états S, A, B, C correspondent respectivement à :

S = nombre pair de a et aucun b
A = nombre impair de a et aucun b
B = nombre pair de a et 1 seul b
C = nombre pair de a et 1 seul b

Donc on démarre dans l'état S, car il y a 0 a et 0 est un nombre pair, si on ajoute un a on passe dans B car il y a un nombre impair de a si on rajoute un a on repasse en S parce qu'il y a de nouveau un nombre pair de a. Si on ajoute un b on passera alors dans l'état B ou C dépendant de l'état d'origine.

Cet automate peut simplement être converti en la grammaire suivante $G = (\{a, b\}, \{ S, A, B, C \}, P, S)$ dont voici les règles de production $P$ :

S → aA
S → bB
A → aS
A → bC
B → aC
B → ε
C → aB