Les langages formels

La théorie des langages formels fut initialement initiée par les linguistes qui tentaient de représenter les langages naturels (exemple, français, anglais, etc). Mais elle s'est révélée être très utile pour l'informatique pour tout un cas d'applications. Notamment les RegEx, et les règles syntaxiques des langages de programmations (avec l'analyse syntaxique).

Un langage naturel va être défini par une orthographe, une grammaire, une conjugaison. Un langage dit formel (tel que les langages de programmations), vont être défini par des règles de constructions. Ainsi, les erreurs syntaxiques d'un code peuvent être détectées grâce à ces mêmes règles de constructions.

La théorie des langages a pour but de décrire les langages formels. Elle ne concerne que les aspects purement syntaxiques du langage. Un langage formel est généralement défini par une grammaire formelle (grammaires algébriques, par exemple) et analysé à l’aide d’automates.

Donc un langage formel va être généré à l'aide d'une grammaire formelle et analysé à l'aide d'un automate.

Alphabets, lettres et mots

L'alphabet est un ensemble fini et non-vide d'éléments appelé lettres ou symboles terminaux. Cet ensemble va être représenté par la lettre $\Sigma$, par exemple : $\Sigma = {a,b,c,1,2,3,if,else}$

• $\Sigma^+$ correspond à l'ensemble de tous les mots sur $\Sigma$
• $\Sigma^* $ correspond à l'ensemble de tous les mots non-vide sur $\Sigma$

Un mot est une séquence finie de lettres. Ainsi dans l'alphabet précédent a, ab et else sont des mots par exemples.

Le mot vide est noté $\varepsilon$ et est défini pour tous les alphabets. Par conséquent, le mot vide ne peut pas être une lettre de l'alphabet $\Sigma$.

Opérations

La concaténation est une opération binaire effectuée sur l'ensemble $\Sigma$ et qui donne un mot obtenu par la concaténation des 2 mots. Elle est associative et non commutative et admet le mot vide $\varepsilon$ comme neutre (donc si $u$ est un mot alors $u = \varepsilon u = u \varepsilon$).

Une concaténation des mots $u$ et $v$ est représentée par $uv$ ou $u * v$ et une concaténation d'un nombre $k$ de $u$ est représentée par $u^k$ donc $uuuuuuuuu = u^9$

Un exposant $+$ correspond à "1 ou plus" (comme en RegEx) tandis qu'un exposant $* $ sur un mot représente "0 ou plus" (toujours comme en regex)

Ainsi $(ab)^+$ signifie que la séquence ab est présente une fois ou plus. Et $(vb)^* $ signifie que la séquence vb est présente 0 fois ou plus.

Une autre opération est qu'un mot peut être retourné en lui mettant un exposant de -1. Donc $(abc)^{-1} = cba$ et un palindrome peut être détecté lorsque $u = u^{-1}$ (par exemple $(radar)^{-1} = (radar)$)

Et on peut aussi récupérer la longueur d'un mot (nombre de symboles terminaux/lettres) comme ceci $|u|$ donc $|(radar)| = 5$

Langage

Un langage est un sous ensemble de $\Sigma^* $ et on peut reconnaitre quelques langages particuliers :

• $\Sigma$ est le langage de tous les mots de longueur 1 sur $\Sigma$
• $\varnothing$ est un langage ne contenant aucun mot
• {$\varepsilon $} est un langage ne contenant que le mot vide
• $\Sigma^+$ langage contenant tous les mots sur $\Sigma^+$
• $\Sigma^* $ langage contenant tous les mots sur $\Sigma^* $

Sur l'ensemble $P(\Sigma^* )$ représentant tous les langages sur $\Sigma^* $ on peut utiliser les opérations ensemblistes habituelles, mais également $\cdot$ permetant de faire un produit des deux langages en utilisant la concaténation sur chaque mot.

Aisni si $L_1 = 1,2,3$ et $L_2 = a,b,c$ et que l'on fait $L_1 \cdot L_2$ on obtient $1a,1b,1c,2a,2b,2c,3a,3b,3c$

On peut utiliser la notation $L^k$ où $k$ est le nombre de lettres, pour représenter une concaténation de k mots du langage L. Et $L^k = L \cdot L^{k-1}$ ainsi :

• $L^0 = \varepsilon$
• $L^1 = L \cdot L^{0} = L \varepsilon = L$
• $L^2 = L \cdot L^{1} = LL$

Pour décrire un langage avec une infinité de mots, on peut utiliser un système générateur (grammaire, RegEx ou diagramme syntaxique) pour générer des mots du langage et des automates finis pour les détecter.

Pour la concaténation de 2 langages, les exposants $+$ (1 ou plus de fois concaténé avec lui-même) et $* $ (0 ou plus de fois concaténé avec lui-même) restent valides, ainsi étant donnés les deux langages :

• $L_1 = ab,ac,c,cb,\varepsilon$
• $L_2 = a,ab,ca,cb,cc$

Quand on applique $(L_1 \cdot L_2)^* $ on peut obtenir des mots tel que acbcb car cela correspond à $(L_1 \cdot L_2)^2 = L_1 \cdot L_2 \cdot L_1 \cdot L_2 = \varepsilon \cdot a \cdot cb \cdot cb = acbcb$. Il faut donc bien penser à tous les mots dans toutes les combinaisons possibles. Mais quand on a un QCM avec plusieurs propositions, quand aucun mot ne commence avec certaines lettres, on peut les éliminer avec certitude, ce qui rend les choses un peu plus simples.

Grammaire

Ici, on va examiner les grammaires dites "de Chomsky" qui représente la forme la plus connue de système de génération de langages, qui sont définies par le quadruplet $G = (\Sigma, N,P,S)$ où les symboles signifient :

• $G$ est la grammaire
• $\Sigma$ est l'ensemble des symboles terminaux (par exemple : Marc, livre, Alice, mange, lit, pomme, une, un)
• $N$ est l'ensemble des symboles non-terminaux (par exemple : sujet, verbe, complément, article, nom)
• $P$ est l'ensemble des productions de la grammaire (c'est-à-dire les associations des symboles non-terminaux avec les symboles terminaux) (exemple, voir la capture d'écran d'une slide ci-dessous). On va voir plus tard que les productions sont des règles de remplacement.
• $S$ est le symbole initial qui entame la génération de la grammaire. Par convention, ce sera $S$ justement

Conventions

• Par convention, les symboles en lettres latines minuscules représentent des symboles terminaux
• Les symboles latins majuscules représentent des symboles non-terminaux
• Les symboles en lettres grecs minuscules représentent des suites de symboles quelconques (terminaux ou pas)
• Les lettres latines minuscules allant de $u$ à $z$ sont considérées comme des suites de symboles terminaux.
• Les lettres latines majuscules allant de $U$ à $Z$ sont considérées comme des symboles quelconques

Dérivation

L'opération de base qui est effectuée dans une grammaire est la dérivation, autrement dit le fait de convertir des symboles non-terminaux en symboles terminaux sur base des règles de production de la grammaire. Cette opération est représentée par le symbole $\Rightarrow$

Ainsi si la grammaire indique que $A \Rightarrow \alpha$ et $S \Rightarrow abcA$ alors la génération de départ donnera $abc\alpha$ car $A$ sera remplacé par $\alpha$

Le langage qui sera généré d'une grammaire est noté $L(G)$ et correspond à l'ensemble $\Sigma$ que l'on peut dériver à partir de la grammaire $G$

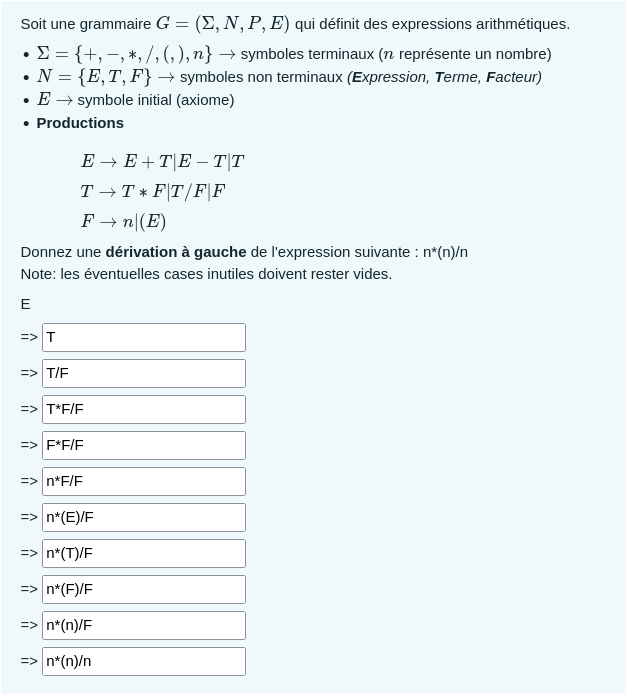
Il y a 2 types de dérivation, la dérivation à gauche et la dérivation à droite, autrement dit que l'on va d'abord s'occuper du terme le plus à gauche ou du terme le plus à droite. Voici un exemple venant des tests :

À savoir que la barre verticale dans ce cas veut dire "ou". Donc la première production veut dire "E peut devenir E+T ou E-T ou T" par exemple.

Dans une dérivation à droite, on aurait à la place toujours commencée par dériver le symbole non terminal le plus à droite.

Grammaire ambigüe

Une grammaire est dite ambigüe si un mot peut être généré par 2 dérivations de gauche non équivalentes. Voici un exemple de grammaire ambigüe :

Donc pour enlever l'ambiguïté, il faut forcer la dérivation dans un certain sens, par exemple avec les nouvelles règles de productions suivante :

𝑆 → if 𝐶 then 𝑆 | if 𝐶 then 𝑇 else 𝑆 | A
𝑇 → if 𝐶 then 𝑇 else 𝑇 | A

Tout langage généré par une grammaire ambigüe est dit intrinsèquement ambigu et ce type de langage est proscrit en informatique.

La dénomination de langage déterministe s'applique à tout langage issu de grammaire non ambigüe.

Les types de grammaires

Il existe différents types de grammaires en fonction de la complexité de leurs règles de productions :

• Type 0 (sans restriction) : les grammaires telles que $\alpha \Rightarrow \beta$ (soit une suite donne une autre)
• Type 1 (contextuelle) : les grammaires telles que $\alpha A\gamma \Rightarrow \alpha\beta\gamma$ (soit un symbole non-terminal est entouré d'au moins 2 mots qui donne le contexte. Le remplacement du symbole terminal va dépendre du contexte dans lequel il se trouve
• Type 2 (algébrique ou non contextuelle) : les grammaires telles que $A \Rightarrow \gamma$ sont la même chose que le type 1 sauf que le contexte est vide
• Type 3 (régulières) : les grammaires telles que $S \Rightarrow aA$ (alors appelée linéaire à droite) ou $S \Rightarrow Aa$ (alors appelée linéaire à gauche). Où le symbole non-terminal d'une règle est toujours placé d'un côté ou de l'autre des symboles non-terminaux. Ce type de grammaire engendre des langages rationnels, c'est-à-dire un langage qui peut être reconnu par un automate fini